Vjylku

АналитическаяЖорданаКантороваУрысонаУникурсальнаяРациональная нормальнаяОвалОвоидДлинаКривизнаВивианиВинтовая линияЛиния откосаЛоксодромаОртодромияПространственная кардиоидаКлелия[en]ГиперболаПараболаЭллипсОкружностьПрямаяЭллиптическая криваяЭллиптические функции ЯкобиЭллиптический интегралЭллиптические функцииВерзьера АньезиДекартов листКубикаТрисектриса МаклоренаЧирнгаузаОфиуридаПолукубическая параболаСтрофоидаТрезубецЦиссоида ДиоклаКаппаКардиоидаУаттаПерсеяОвал ДекартаБернуллиОвал КассиниБутаЖероноСплайнB-сплайнКубическийМоносплайнСглаживающийСовершенныйЭрмитаБезьеКардиоидаНефроидаДельтоидаАстроидаУлитка ПаскаляКривая ФермаКубическаяАрхимедоваФермаГалилеяГиперболическая«Жезл»ЗолотаяКлотоидаЛогарифмическаяСинусоидальнаяЦиклоидаЭпициклоидаГипоциклоидаТрохоидаУдлинённаяУкороченная циклоидаЭпитрохоидаУдлинённаяУкороченная эпициклоида«Роза»КвадрифолийГипотрохоидаКвазитрохоидаСкорейшего спуска (Брахистохрона, дуга циклоиды)КвадратрисаКохлеоидаПогониТрактрисаТрохоидаЦепная линияперевёрнутая арочнаяПостоянной шириныСинусоидаРибокураСуперформулаСуперэллипсТреугольник РёломногоугольникФигуры ЛиссажуГильбертаГоспераКривая драконаКохаЛевиМинковскогоПеаноСерпинскогоСалфетка СерпинскогоКовёр СерпинскогоГубка МенгераКруговой фракталСетка Аполлония

Алгебраические кривые

алгебраическая криваяпрямоугольнойНейла1657 годукаустикойкривой Чирнгаузеналасточкин хвосттеории катастрофРадиус кривизны

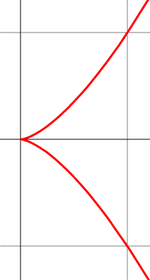
Полукубическая парабола

Полукубическая парабола, или парабола Нейла, — плоская алгебраическая кривая, описываемая уравнением y²=ax³ в некоторой прямоугольной системе координат. Названа по имени Нейла, который в 1657 году вычислил длину её дуги.

Уравнения |

• Алгебраическое уравнение: y²=ax³ (a≠0).


• Параметрическое уравнение: x=t², y=at³ (a≠0).

Свойства |

Полукубическая парабола является каустикой кривой Чирнгаузена. Более того, любая каустика вида «ласточкин хвост» вблизи вершины хорошо приближается полукубической параболой, что делает эту кривую эталонной в теории катастроф.

Радиус кривизны полукубической параболы в начале координат равен нулю.

Это заготовка статьи по математике. Вы можете помочь проекту, дополнив её.